洛倫茲曲線研究的是國民收入在國民之間的分配問題。為了研究國民收入在國民之間的分配問題，美國統(tǒng)計學家（或說奧地利統(tǒng)計學家）M.O.洛倫茲（Max Otto Lorenz，1903- ）1907年（或說1905年）提出了著名的洛倫茲曲線。意大利經(jīng)濟學家基尼在此基礎上定義了基尼系數(shù)。

畫一個矩形，矩形的高衡量社會財富的百分比，將之分為五等份，每一等分為20的社會總財富。在矩形的長上，將100的家庭從最貧者到最富者自左向右排列，也分為5等分，第一個等份代表收入最低的20的家庭。在這個矩形中，將每一百分的家庭所有擁有的財富的百分比累計起來，并將相應的點畫在圖中，便得到了一條曲線就是洛倫茲曲線。

顯而易見，洛倫茲曲線的彎曲程度具有重要意義。一般來說，它反映了收入分配的不平等程度。彎曲程度越大，收入分配程度越不平等；反之亦然。特別是，如果所有收入都集中在某一個人手中，而其余人口均一無所有，收入分配達到完全不平等，洛倫茲曲線成為折線OHL；另一方面，如果任一人口百分比等于其收入百分比，從而人口累計百分比等于收入累計百分比，則收入分配就是完全平等的，洛倫茲曲線成為通過原點的45度線OL。

洛倫茲曲線用以比較和分析一個國家在不同時代或者不同國家在同一時代的財富不平等，該曲線作為一個總結收入和財富分配信息的便利的圖形方法得到廣泛應用。

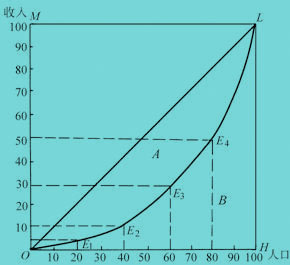
圖中橫軸OH表示人口（按收入由低到高分組）的累積百分比，縱軸OM表示收入的累積百分比，弧線OL為洛倫茲曲線。

洛倫茲曲線的彎曲程度有重要意義。一般來講，它反映了收入分配的不平等程度。彎曲程度越大，收入分配越不平等，反之亦然。特別是，如果所有收入都集中在一人手中，而其余人口均一無所獲時，收入分配達到完全不平等，洛倫茲曲線成為折線OHL.另一方面，若任一人口百分比均等于其收入百分比，從而人口累計百分比等于收入累計百分比，則收入分配是完全平等的，洛倫茲曲線成為通過原點的45度線OL。

一般來說，一個國家的收入分配，既不是完全不平等，也不是完全平等，而是介于兩者之間。相應的洛倫茲曲線，既不是折線OHL，也不是45度線OL,而是像圖中這樣向橫軸突出的弧線OL，盡管突出的程度有所不同。

將洛倫茲曲線與45度線之間的部分A叫做“不平等面積”，當收入分配達到完全不平等時，洛倫茲曲線成為折線OHL，OHL與45度線之間的面積A+B叫做“完全不平等面積”。不平等面積與完全不平等面積之比，成為基尼系數(shù)，是衡量一國貧富差距的標準?；嵯禂?shù)G=A/(A+B).顯然，基尼系數(shù)不會大于1，也不會小于零。

盡管可根據(jù)收入分配的統(tǒng)計數(shù)據(jù)加以描繪，但至今卻未能找到一種有效的方法，準確地擬合洛倫茲曲線方程并由此求出精確的基尼系數(shù)。目前常被使用的方法主要有三種：

(1)幾何計算法。即根據(jù)分組資料,按幾何圖形分塊近似逼近計算的方法。

(2)間接擬合法。即先擬合求出收入分配的概率密度函數(shù)，再根據(jù)概率密度函數(shù)導出洛倫茲曲線。

(3)曲線擬合法，即選擇適當?shù)那€直接擬合洛倫茲曲線，常用的曲線有二次曲線、指數(shù)曲線和冪函數(shù)曲線。

利用第一種方法不能得到洛倫茲曲線的表達式，只能用來計算基尼系數(shù)，但由于在計算分塊面積時用直線近似地代替曲線，所估計的基尼系數(shù)要小于實際值，尤其在數(shù)據(jù)點較少時，誤差較大。第二種方法由于計算收入分配的概率密度的復雜性,很難提出合適的概率函數(shù)。至于第三種方法，即直接用曲線方程去擬合洛倫茲曲線，應該不失為一種較好的方法，但目前主要的問題在于現(xiàn)有常用的曲線并不適用，曲線含義不明確，或擬合誤差較大。

為了更準確地描述洛倫茲曲線和精確地估計基尼系數(shù)，我們通過分析洛倫茲曲線的特性，設計出一條洛倫茲曲線方程，對洛倫茲曲線直接進行擬合。經(jīng)過實例分析，擬合效果好，由洛倫茲曲線可推導出基尼系數(shù)的計算公式，計算結果精確度也很高。